Die Entwicklung eines umfassenden Operationsverständnisses der Multiplikation gehört zu einer zentralen Aufgabe des Mathematikunterrichts der Grundschule. Die Lernenden sollen im Laufe der Zeit ihre Vorstellungen zur Multiplikation ausbauen und die Bedeutungsvielfalt dieser Rechenoperation erfassen.
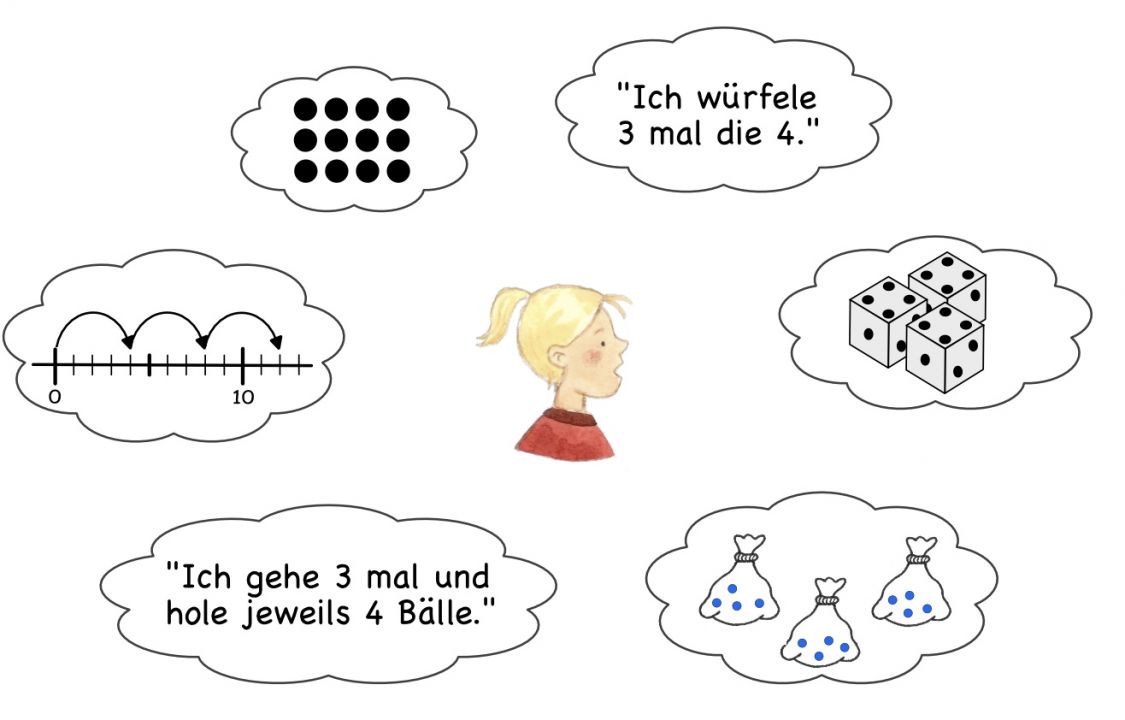
Bereits vor Schuleintritt verfügen Kinder über lebensweltliche Handlungserfahrungen, ohne diese natürlich bewusst als Multiplikation wahrzunehmen. Durch Formulierungen wie „2mal schlafen“, „5mal hüpfen“ usw. lernen Kinder die Bedeutung von „mehrmals etwas tun“ kennen. Auch im Kontext von Spielen begegnet ihnen das Wort „mal“ häufig: „Du darfst 3mal würfeln.“ Folglich haben sie oftmals intuitiv bereits verknüpft, dass mit dem Wort „mal“ die Wiederholung einer Handlung verbunden ist. In der Schuleingangsphase lernen die Kinder dann, dass sich die Anzahl mehrerer gleichgroßer Mengen durch eine wiederholte Addition ermitteln lässt (3 + 3 + 3 + 3). Diese Vorstellung wird im Mathematikunterricht erweitert und mit der Multiplikation als Verkürzung der wiederholten Addition verknüpft. Im Unterricht lassen sich multiplikative Situationen nachspielen oder durch die Verknüpfung von bildlichen Darstellungen und symbolischen Schreibweisen (Additions- und Multiplikationsaufgabe) beispielsweise anhand einer Fotokartei oder des Zuordnungsspiels Mal-Trio fördern. Ziel sollte die Förderung eines umfassenden Operationsverständnisses der Multiplikation sein. Dafür ist es wesentlich, dass die Kinder im Unterricht:

Zur Entwicklung der Grundvorstellungen der Multiplikation spielen die zeitlich-sukzessive sowie die räumlich-simultane Grundvorstellung eine zentrale Rolle. Die Lernenden sollen die Multiplikation in unterschiedlichen Kontexten erfahren als:

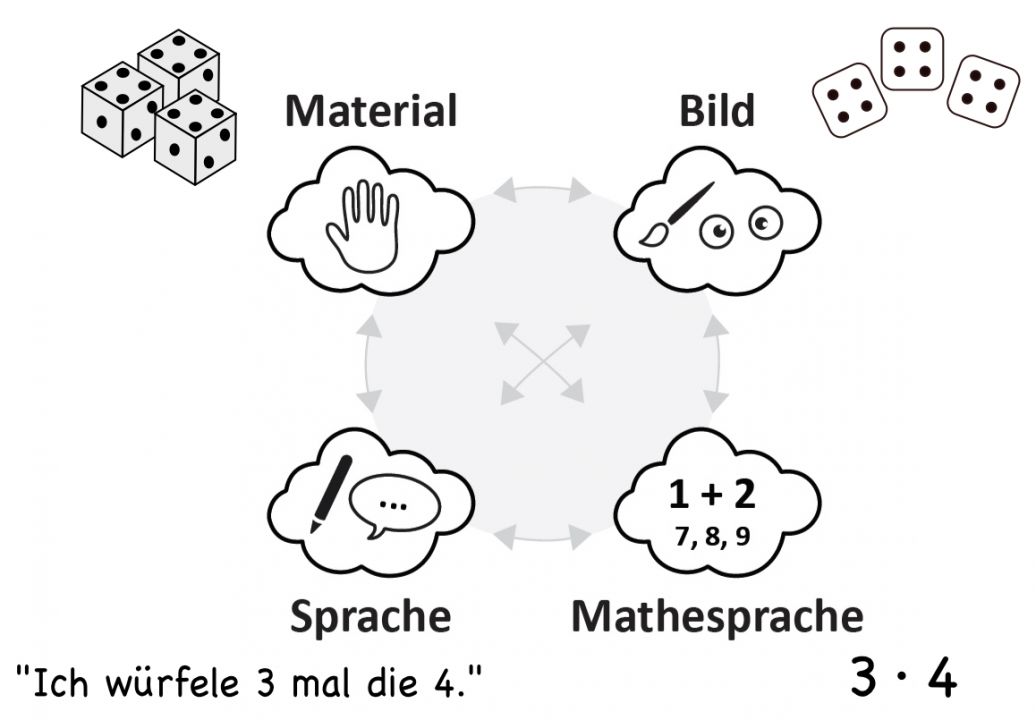
Für einen verstehensbasierten Umgang mit der Multiplikation ist es entscheidend, dass das Rechnen nicht bloß auf der symbolischen Ebene erfolgt, sondern immer auch mit Vorstellungen von Handlungen und Sachsituationen verbunden ist. Für die Lernenden ist es daher wichtig, multiplikative Zusammenhänge in verschiedenen Darstellungen zu erkennen und zwischen diesen flexibel wechseln zu können. Die folgende Grafik verdeutlicht unterschiedliche Darstellungsformen der Multiplikation. Zunächst ist es wesentlich, dass die Multiplikation in verschiedenen Darstellungen im Unterricht erarbeitet wird. Darauf aufbauend können unterschiedliche Übungen (Material) genutzt werden, um den Darstellungswechsel zu trainieren.
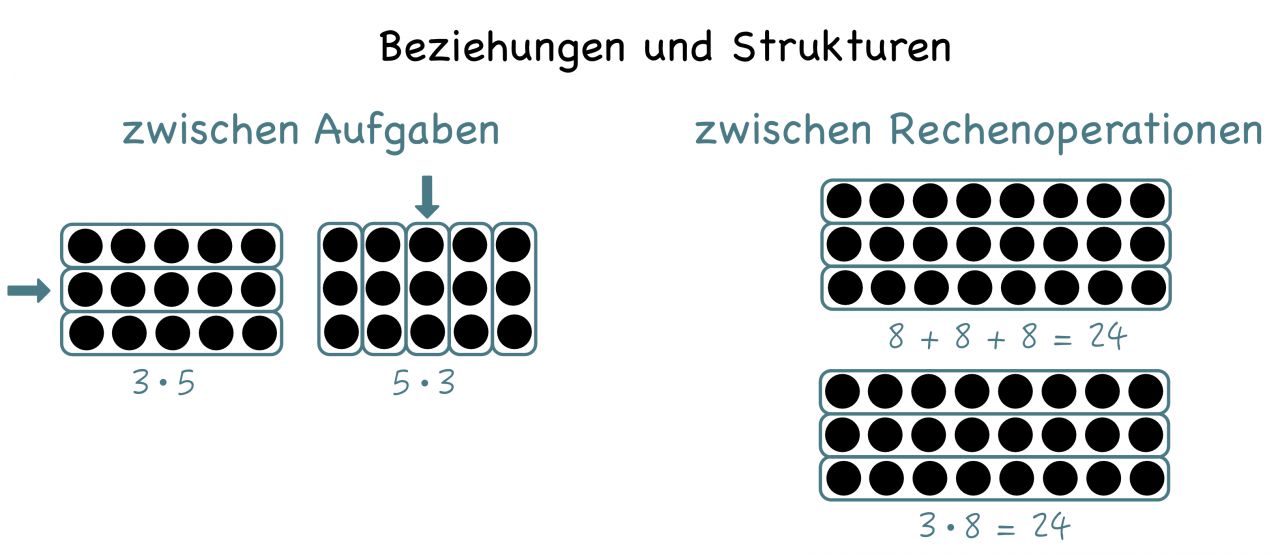
Für die Entwicklung eines umfassenden Operationsverständnisses sollen Lernende zudem Gelegenheiten bekommen, Beziehungen und Strukturen entdecken und diese für das sichere und flexible Rechnen nutzen zu können. Materialgestützt bietet die Multiplikation verschiedene Möglichkeiten, Beziehungen und Strukturen zwischen Aufgaben sowie zwischen Rechenoperationen zu erkunden.
Unter Berücksichtigung der Aspekte "Grundvorstellungen entwickeln, Darstellungswechsel durchführen und Beziehungen und Strukturen nutzen" bei der Unterrichtsplanung bietet das Thema Multiplikation vielfältige Möglichkeiten, über das formale Rechnen hinaus, die Entwicklung eines umfassenden Operationsverständnisses der Multiplikation anzuregen.
Im Folgenden wird die Multiplikation dargestellt als:
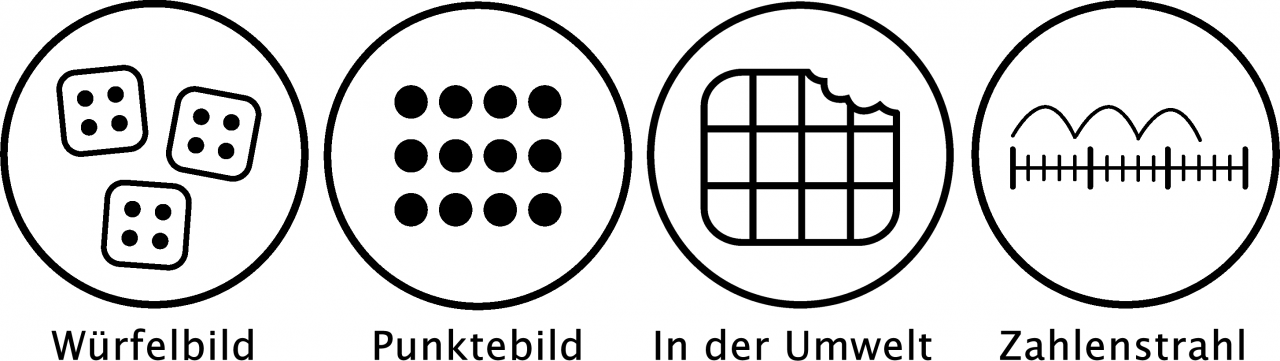
In den folgenden Dokumenten wird zu diesen Darstellungsformen der Multiplikation jeweils eine Ausgangsaufgabe aus dem Blickwinkel der vier Schwerpunktthemen Prozessbezogene Kompetenzen ausbauen, Matheschwierigkeiten begegnen, Sprachbildend unterrichten und Mathestärken fördern betrachtet und diese anhand exemplarischer Unterrichtsanregungen für die Umsetzung im Unterricht konkretisiert.
Ausgangsaufgabe
Zeichne zu drei Würfeln die Würfelbilder mit gleichen Augenzahlen.
Welche Würfelbilder findest du?
Am Beispiel der Würfelbilder kann sowohl die multiplikative Vorstellung der Wiederholung als auch des Zusammenfassens verdeutlicht werden, indem aus der zeitlich-sukzessiven Handlung des Würfelns (Ich würfele einmal vier, zweimal vier, dreimal vier.) das räumlich-simultane Würfelbild dreimal vier abgeleitet wird. Es lässt sich veranschaulichen, dass die Multiplikation eine verkürzte Schreibweise der wiederholten Addition gleicher Summanden darstellt. Zudem wird die entstehende gruppierte Darstellung genutzt, um das grundlegende Verständnis der Multiplikation als Zusammenfassung gleichmächtiger Gruppen zu entwickeln. Die Gruppenbildung kann sprachlich durch die Gruppensprache (Ich sehe 3 Vierer) hervorgehoben werden und unterstützt die Lernenden somit in ihrer Vorstellungsentwicklung.
Ausgangsaufgabe
Finde Mal-Aufgaben in deiner Umgebung.
Zeichne/fotografiere sie und notiere die Mal-Aufgabe.
Lernende, die ein umfassendes Operationsverständnis der Multiplikation entwickeln, sollen Multiplikation nicht nur im offensichtlich mathematischen Kontext, beispielsweise am Punktefeld oder Zahlenstrahl, erkennen und anwenden können. Ebenso wichtig ist es, dass sie Multiplikation auch in der Umwelt entdecken und somit Realsituationen, Bilder oder auch Rechengeschichten mit Multiplikationsaufgaben in Beziehung setzen können. Im Vordergrund stehen dabei Begründungen der Lernenden zu der Frage:„Warum passen Mal-Aufgabe und Bild zusammen?“ Durch die Verknüpfung von Mathematik und alltagsweltlichem Bezug erweitert sich bei den Lernenden die Vorstellung der Multiplikation und wird für verschiedene Sachsituationen anwendbar.
Operationsverständnis Multiplikation - In der Umwelt
Ausgangsaufgabe
Wähle eine Mal-Aufgabe und zeichne dazu ein passendes Punktebild.
Punktefelder eignen sich besonders, um die flächige Vorstellung der Multiplikation zu entwickelt und um Rechengesetze zu veranschaulichen. Im Punktefeld sind beide Faktoren sowie das Produkt sichtbar. Abhängig von der Perspektive des Betrachters lässt sich die Multiplikationsaufgabe sowie die Tauschaufgabe am Punktefeld entdecken und somit das Kommutativgesetz erarbeiten. Beim Darstellungswechsel von der flächigen Darstellung in einen Term wird meist die Anzahl der Zeilen durch den Multiplikator und die Anzahl der Spalten durch den Multiplikanden angegeben. Gemeinsam mit den Lernenden sollte thematisiert werden, dass es sich dabei nur um eine Vereinbarung handelt, um eindeutiger kommunizieren zu können. Bedeutend ist ein grundsätzlich flexibler Blick auf das Punktefeld.
Ausgangsaufgabe
Wähle eine Mal-Aufgabe und zeichne die Sprünge am Zahlenstrahl ein.
Für die Entwicklung linearer Vorstellungen zur Multiplikation kann der Zahlenstrahl genutzt werden, an welchem sich die Multiplikation anschaulich als eine Reihe gleichgroßer Sprünge darstellen lässt. Am Zahlenstrahl lassen sich dann sowohl das Produkt als auch beide Faktoren der Multiplikation ablesen. Wichtig ist es dabei, die unterschiedliche Rolle der Faktoren Multiplikand und Multiplikator zu berücksichtigen. In der Grundschule steht dabei nicht die begriffliche Bezeichnung von Multiplikand und Multiplikator im Fokus, sondern vielmehr die Veranschaulichung der unterschiedlichen Bedeutung von der Anzahl der Sprünge und der Länge der Sprünge.
Operationsverständnis Multiplikation - Zahlenstrahl
Weiteres Material finden Sie auf den Partnerprojektseiten mit dem Materialfinder
Testen Sie Ihr Wissen zu dem Thema mit unserem Kira-Check