Bereits 2005 wurde in den KMK Bildungsstandards (2005, S. 6) als Ziel des Mathematikunterrichts die "Entwicklung eines gesicherten Verständnisses mathematischer Inhalte" (ebd., S. 6) beschrieben. Dabei sollen die Schülerinnen und Schüler sowohl inhalts- als auch prozessbezogene Kompetenzen erwerben. Im Mathematiklehrplan des Landes NRW für die Grundschule (vgl. MSW NRW, 2008, S. 61-66) wird dabei zwischen folgenden inhaltsbezogenen Kompetenzbereichen unterschieden:
-
Zahlen und Operationen
-
Raum und Form
-
Messen und Größen
-
Daten, Häufigkeiten, Wahrscheinlichkeiten
Die Förderung der prozessbezogenen Kompetenzen soll dazu beitragen, dass eine verständnisorientierte, mathematische Grundbildung anvisiert wird. Prozessbezogene Kompetenzen sind somit "für eine erfolgreiche Nutzung und Aneignung von Mathematik von zentraler Bedeutung" (KMK, 2005, S. 7). Während in den Bildungsstandards von allgemeinen mathematischen Kompetenzen gesprochen wird, die das Problemlösen, das Kommunizieren, das Argumentieren, das Modellieren und das Darstellen umfassen, nutzt der Mathematiklehrplan des Landes NRW den Begriff prozessbezogene Kompetenzen und es werden dort vier Kompetenzbereiche benannt, da die beiden Kompetenzen Darstellen und Kommunizieren in einem Bereich zusammengefasst werden. Dadurch ergeben sich folgenden prozessbezogene Kompetenzbereiche:
-
Problemlösen/kreativ sein
-
Modellieren
-
Argumentieren
-
Darstellen/Kommunizieren
(vgl. MSW NRW, 2008, S. 59-60)
Weitere Informationen zu den prozessbezogenen Kompetenzen finden Sie unter:
-
primakom: Grundlageninformationen prozessbezogene Kompetenzen
-
PIKAS: PIK-Plakat - Kinderlehrplan
-
PIKAS: Forschermittelplakat
-
PIKAS: Förderung prozessbezogener Kompetenzen mit Forschermitteln
-
PIKAS: Informationsvideo inhalts- und prozessbezogene Kompetenzen
Beim Problemlösen handelt es sich um zielgerichtetes Denken und Handeln, in Situationen, in denen eine Diskrepanz zwischen den vorhandenen Mitteln und den Aufgabenanforderungen wahrgenommen wird (vgl. Selter & Zannetin, 2018, S. 12). Ob eine Lernaufgaben demnach eine Aufgabe zum Problemlösen darstellt, hängt wesentlich auch von den individuellen Kenntnissen und Fertigkeiten des jeweiligen Kindes ab, das sich mit der Aufgabe auseinandersetzt.
das Bild ist zu klein und hat einen weißen Bereich, dadurch erscheint es nicht linksbündig
Bei der Aufgabe, verschiedenes Geschenkpapier (grün, blau und gelb) mit unterschiedlichen Schleifen (rot, blau und grün) miteinander zu kombinieren (PIKAS: Material für besondere Anlässe), gehen manche Kinder evtl. bereits von Beginn an systematisch vor und legen oder zeichnen zunächst alle Möglichkeiten mit Papier derselben Farbe, wobei sie nur die Schleifen austauschen. Andere Kinder wiederum werden unsystematisch einzelne Möglichkeiten legen oder notieren und erst durch den Vergleich ihrer Möglichkeiten einen Blick auf Zusammenhänge richten und zunehmend systematisch vorgehen (vgl. primakom: Problemlösen).
Daher ist es notwendig, sich über die Lernstände der Kinder bewusst zu sein und die Problemlöseaufgaben individuell zu variieren. Problemlöseaufgaben sollten den Lernenden daher die Möglichkeit geben, verschiedene Vorgehensweisen auf unterschiedlichen Niveaus entwickeln zu können und das Problem oder Teile des Problems lösen zu können.
Selter & Zannetin (2018, S. 13) konkretisieren dei Kompetenzerwartungen in Anlehnung an den Lehrplan NRW (S. 59) wie folgt:
-
Erschließen: Fragen zu mathematischen Sachverhalten stellen; Problemstellungen die für die Lösung relevanten Informationen entnehmen; Problemstellungen in eigenen Worten wiedergeben
-
Lösen: Daten durch Zählen, Messen oder Schätzen gewinnen und verarbeiten; problemhaltige Aufgaben eingeständig bearbeiten; zunehmend systematisch und zielorientiert vorgehen; Lösungsstrategien anwenden; Einsichten in Zusammenhänge zur Problemlösung nutzen
-
Reflektieren und Überprüfen: Ergebnisse auf Angemessenheit überprüfen; Fehler finden und korrigieren; verschiedene Lösungswege vergleichen und bewerten
-
Übertragen: Einsicht in Zusammenhänge zur Problemlösung nutzen; Vorgehensweisen auf ähnliche oder weiterführende Problemstellungen übertragen
-
Erfinden: Aufgaben (in Anlehnung an vorgegebene) erfinden; eigene Lösungsstrategien entwickeln und nutzen
Die Schlagwörter Erschließen, Lösen, Reflektieren, Überprüfen, Übertragen, Erfinden weisen dabei darauf hin, welche Teilkompetenzen die Lehrkraft im Blick haben sollte, um die Lernenden mit möglichen und nötigen Impulsfragen, sowie einzelnen Arbeitsaufträgen zu unterstützen.
Weitere Informationen zum Kompetenzbereich Problemlösen finden Sie unter:
-
primakom: Grundlageninformationen Problemlösen
-
PIKAS: Haus 7 Aufgaben zum Problemlösen
Nach Krauthausen und Scherer (2007) wird mit dem Begriff des Darstellens jegliche Art der "Veräußerung des Denkens" verbunden. Das bedeutet, dass beim Darstellen innere Überlegungen zu mathematischen Sachverhalten auf verschiedenen Repräsentationsebenen (Handlungsabläufe, Bilder, Sprache, Symbole) wiedergegeben werden. Für die Multiplikation und hier insbesondere die Aufgaben 2 • 5 und ihre Tauschaufgabe 5 • 2 könnte dies wie folgt aussehen:
das Bild hat einen weißen Bereich links und ist etwas unscharf
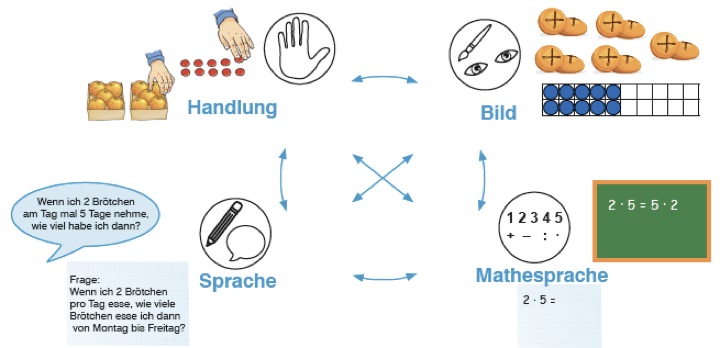 Abb. aus: Selter & Zannetin, 2018, S. 46
Abb. aus: Selter & Zannetin, 2018, S. 46
D.h., dass mathematische Sachverhalte sowohl durch materiale, bildliche, verbalsprachliche, als auch symbolsprachliche Repräsentationen wiedergegeben werden können. Bevor die Lernenden diese verschiedenen Repräsentationen, die im Folgenden mit dem Begriff Darstellungen gleichgesetzt werden, jedoch flexibel nutzen können und auch zwischen den Darstellungen wechseln können, sollten ihnen immer wieder Darstellungsmittel zur Verfügung gestellt werden.
Dabei ist es wichtig, den Umgang mit den Darstellungsmitteln zu thematisieren, denn "jede dieser Hilfen ist zunächst einmal selbst Lernstoff, bevor sie als Werkzeuge genutzt werden können." (vgl. sinus, S. 8). Darüber hinaus bietet es sich an, den situationsgerechten Einsatz bestimmter Darstellungen von Kindern beschreiben und begründen zu lassen. "Ich habe die Aufgabe 5 • 6 mit den Plättchen so gelegt, weil ... ."
Das Darstellen ist daher eng mit dem Kommunizieren und Kooperieren verknüpft, da auf diese Weise durch die verbalsprachliche Repräsentation und den Austausch über verschiedene Sichtweisen auf Darstellungen, dem inneren Denkprozess Ausdruck verliehen wird. Die Lernenden benötigen daher eine geeignete Auswahl und auch vielfältige Vernetzungen der verschiedenen Darstellungsmöglichkeiten, sowie vielfältige Möglichkeiten zum gemeinsamen Austausch, bespielsweise im Sinne des dialogischen Lernens nach Gallin und Ruf (PIKAS: Text "Dialogisches Lernen von Sprache und Mathematik"), um ihre Kompetenezen im Darstellen zu entwickeln und zu festigen.
Selter & Zannetin (2018, S. 17) konkretisieren die Kompetenzerwartungen in Anlehnung an den Mathematiklehrplan NRW (2008, S. 60) wie folgt:
-
Darstellungen auswählen und nutzen: geeignete Darstellungsformen für das Bearbeiten mathematischer Probleme entwickeln und als Kommunikationshilfe nutzen; geeignete Darstellungen wählen, um Informationen übersichtlich wiederzugeben; Arbeitsergebnisse und Lernerfahrungen festhalten
-
Darstellungen vernetzen: Darstellungen vergleichen und bewerten; Darstellungen in andere Darstellungen übertrage; zwischen Darstellungen wechseln
-
Unterrichtssprache verwenden: zur Darstellung mathematischer Sachverhalte geeignete Fachbegriffe, mathematische Zeichen und Konventionen sachgeracht verwenden
-
Kommunizieren und kooperieren: komplexe Aufgaben gemeinsam bearbeiten; Verabredungen treffen und einhalten; eigene und fremde Standpunkte in Beziehung setzen
Vor allem in den Häusern Operationsverständnis Multiplikation und Zahlverständnis Anfangsunterricht werden die oben genannten Teilkompetenzen zum Darstellen und Kommunizieren mit konkreten Aufgabenbeispielen und Impulsfragen gefordert und gefördert.
Weitere Informationen zum Kompetenzbereich Darstellen und Kommunizieren finden Sie unter:
-
primakom: Grundlageninformationen zum Darstellen
-
primakom: Operationsvorstellungen mit Schwerpunkt Darstellungswechsel
-
primakom: Grundlageninformationen zum Kommunizieren
Die zentrale Bedeutung des Argumentierens im Mathematikunterricht der Primarstufe wird in den Bildungsstandards (KMK, 2005, S. 8) wie folgt beschrieben: "mathematische Aussagen hinterfragen und auf Korrektheit prüfen, mathematische Zusammenhänge erkennen und Vermutungen entwickeln, Begründungen suchen und nachvollziehen."
der Text im Bild ist nicht lesbar
Hier wird deutlich, dass Mathematik keine bloße Ansammlung von Wissen und Können darstellt, sondern eine menschliche Aktivität, eine Tätigkeit, eine Geisteshaltung ist (vgl. Freudenthal, 1982). Der Mathematikunterricht der Primarstufe sollte demnach nicht nur dazu anregen vorgegebene Wissenselemente und Handlungsanweisungen zu reproduzieren, sondern vielmehr mathematische Muster (Beziehungen, Ordnungen, Zusammenhänge, Strukturen, Auffälligkeiten, Abhängigkeiten oder Regelmäßigkeiten) zu "erforschen, fortzusetzen, auszugestalten und selbst zu erzeugen" (Wittmann, 2003, S. 26).
Im Sinne einer Förderung der Kompetenzen im Bereich des Argumentierens wäre eine Beschränkung auf das Erkennen und das Beschreiben solcher Muster nicht ausreichend.
der Text im Bild ist nicht lesbar
Nach Wittmann und Müller (2007, S. 49) sollen Muster auch "unter Forschern kommuniziert und zur Lösung realer Probleme genutzt werden." Eine Argumentation erfolgt dabei einerseits, um sich selbst zu überzeugen, aber auch um andere zu überzeugen.Dabei können die Lernenden zum einen miteinander argumentieren ("Wir überlegen gemeinsam, warum das so ist") oder gegeneinander ("Wer von uns hat warum Recht?") (vgl. Selter & Zannetin, 2018, S. 15).
Vor allem beim Widerlegen einer Vermutung werden die Kinder dazu angeregt Gegenbeispiele zu finden und eine Aussage zu überprüfen. Die oben genannten Teilkompetenzbereiche konkretisieren Selter & Zannetin (2018, S. 15) in Anlehnung an den Mathematiklehrplan NRW (2008, S. 60) wie folgt:
-
Beschreiben: Beziehungen und Gesetzmäßigkeiten an Beispielen ansatzweise aufgrund allgemeiner Überlegungen erklären; eigene Vorgehensweisen und Lösungswege verständlich angeben
-
Vermuten: Vermutungen über mathematische Zusammenhänge und Auffälligkeiten anstellen; Vermutungen anhand von Beispielen testen
-
Begründen: eigenen Vorgehensweisen und Lösungswege begründen; Begründungen anderer nachvollziehen; Vermutungen anhand von Beispielen bestätigen oder widerlegen; allgemeine Überlegungen nachvollziehen und entwickeln
-
Überprüfen: Vermutungen, Lösungen sowie eigene und Aussagen anderer hinterfragen
Eine derartige "Aufzählung von Tätigkeiten bietet mehr als ein Beobachtungsraster für Lernprozesse. Wird sie in all ihren Punkten ernst genommen, so wird sie gleichsam zum Leitfaden für die Setzung unterrichtlicher Anregungen und darüber hinaus zur "Checkliste" für Aufgabenstellungen" (vgl. Steinweg, 2014, S. 57). Dabei kann es beispielsweise Lernaufgaben geben, die alle Teilkompetenzen abdecken. Es ist aber auch möglich die "Checkliste" durch verschiedene Aufgabenstellungen in den Blick zu nehmen.
Die aufgeführten Teilkompentenzen werden in dem Unterrichtsbeispiel Würfelbilder (Operationsverständnis Multipliaktion) bei Pikas kompakt aufgegriffen und durch vielfältige Aufgabenstellungen konkretisiert, um die Kompetenzen im Bereich Argumentieren zu fördern und zu fordern.
Weitere Informationen zum Kompetenzbereich Argumentieren finden Sie unter:
-
primakom: Grundlageninformationen zum Argumentieren
Beim Modellieren stehen Lernende vor der Situation, Mathematik auf eine konkrete Aufgabenstellung der Erfahrungswelt anzuwenden (Bifie, 2012, S. 9). Das bedeutet, dass die vorliegende Aufgabe den Lernenden die Möglichkeit geben sollte aus Sachsituationen relevante Informationen zu erfassen, die Problemstellungen aus Sachsituationen in ein mathematisches Modell zu übersetzen, mithilfe des Modells zu lösen, die Ergebnisse wieder auf die Sachsituation zu beziehen und auf Plausibilität zu prüfen.
In Anlehnung an den Mathematiklehrplan NRW (2008, S. 59) konkretisieren Selter & Zannetin (2018, S. 19) die Kompetenzerwartungen im Bereich Modellieren wie folgt:
-
Erfassen: Bildern, Sachtexten und anderen Darstellungen der Lebenswirklichkeit und Sachaufgaben Informationen entnehmen; zwischen relevanten und nicht relevanten Informationen entscheiden
-
Mathematisieren: Problemstellungen aus Sachsituationen in ein mathematisches Modell übersetzen
-
Lösen: Problemstellungen mithilfe des Modells (z. B. Gleichung, Tabelle, Zeichnung) lösen
-
Interpretieren und validieren: Ergebnisse auf Sachsituationen beziehen und auf Plausibilität prüfen; zu gegebenen mathematischen Modellen passende Problemstellungen finden
Ein mögliches Aufgabenformat, um das Modellieren bei Kindern zu beobachten und zu fördern, stellt beispielsweise „Kann das stimmen?“ – Aufgaben dar. Diese können der sogenannten Zeitungsmathematik zugeordnet werden (vgl. Herget & Scholz, 1998). Im Wesentlichen werden hier Aussagen in Zeitungsartikeln auf ihre Plausibilität geprüft (KIRA: Zeitungsmathematik).
der Text im Bild ist grenzwertig klein, warum wird hier ein Bild verwendet? es enthält nur Text!
Bezogen auf die oben genannten Kompetenzerwartungen, die in einem Modellierungskreislauf veranschaulicht werden können, bedeutet das, dass die Lernenden bei der oben genannten Aufgabe zunächst überlegen müssen, welche Informationen für die Lösung der Aufgabe relevant sind. Sie müssen herausfinden, ob es in 10 Jahren möglich ist 1000 Mal die Kindersendung Blinky zu schauen. D.h. die Lernden können sich mit der Frage auseinandersetzen, wie häufig die Sendung in 10 Jahren läuft. Diese Fragestellung können sie nun in verschiedenen mathematischen Modellen (Rechenaufgabe, Zeichnung, Tabelle, etc.) lösen. Da die Sendung nur einmal in der Woche läuft, könnten die Lernenden überlegen, wie viele Wochen ein Jahr hat und dann 10 Jahre mit 52 Wochen multiplizieren. Auf diese Weise stellen sie fest, dass die Sendung nur 520mal in 10 Jahren gelaufen sein kann. Dieses Ergebnis müssen die Lernenden nun wieder auf die Sachsituation beziehen und stellen fest, dass die Aussage nicht stimmen kann.
Text im Bild ist nicht lesbar
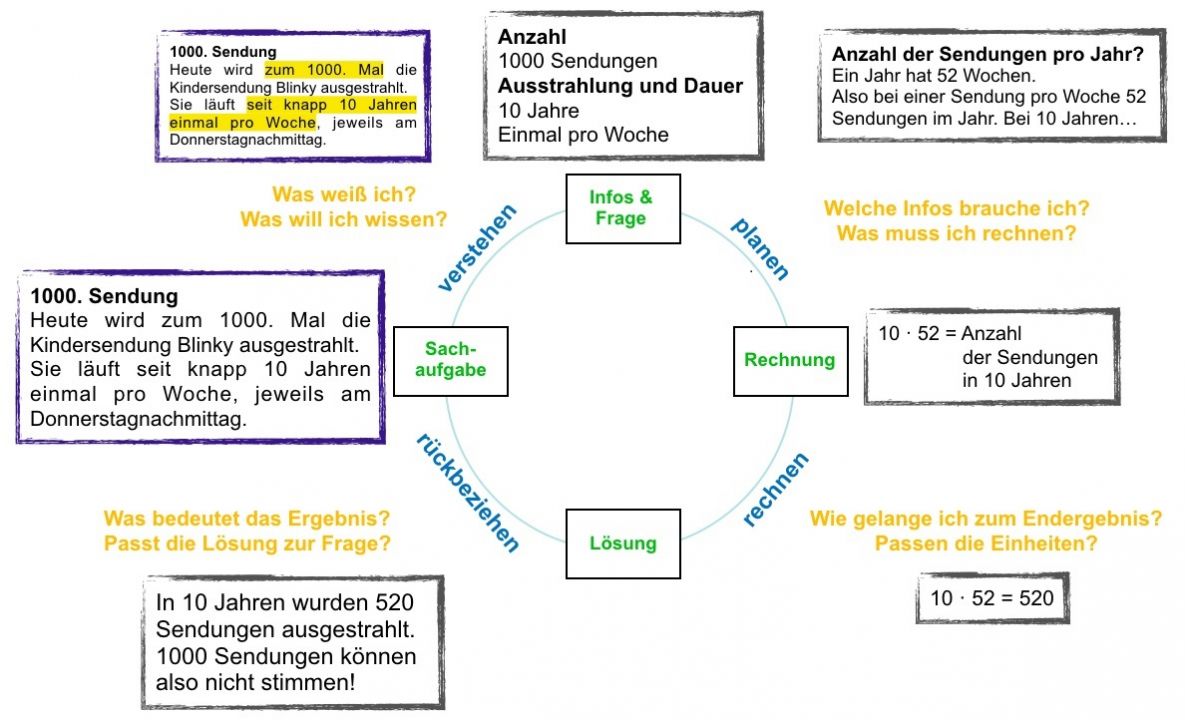 Modellierungskreislauf an einer Beispielaufgabe
Modellierungskreislauf an einer Beispielaufgabe
Die Kinder werden durch derartige Problemstellungen zum Modellieren angeregt, können ihr Stützpunktwissen erweitern, lernen Zeitungsartikel kritisch zu hinterfragen, und Basiswissen, wie Überschlagsrechnen, Nutzen verschiedener Rechenoperationen, u.a. wird angewandt. Der Modellierungskreislauf ist dabei nicht als strikter Ablaufplan zu verstehen, sondern er beschreibt wesentliche Elemente des Lösungsprozesses, zwischen denen gewechselt wird und die unter Umständen auch mehrfach realisiert werden (vgl. Selter & Zannetin, 2018, S. 18).
Weitere Informationen zum Modellieren finden Sie unter:
-
primakom: Grundlageninformationen zum Modellieren
-
PIKAS: Text "Fermiaufgaben"
-
KIRA: Bauernhofaufgabe - eine Modellierungsaufgabe
-
KIRA: Kann das stimmen?
„Kinder an schulische Leistungsanforderungen und den produktiven Umgang mit der eigenen Leistungsfähigkeit heranzuführen, ist eine wesentliche Aufgabe der Grundschule. Dabei ist sie einem pädagogischen Leistungsverständnis verpflichtet, das Leistungsanforderungen mit individueller Förderung verbindet. Für den Unterricht bedeutet dies, Leistungen nicht nur zu fordern, sondern sie auch zu ermöglichen, wahrzunehmen und zu fördern“ (MSW NRW, 2008, S. 16).
Für den Mathematikunterricht der Grundschule bedeutet dies, dass es neben der Orientierung an pädagogischen Leitideen im Sinne einer pädagogischen Leistungskultur (vgl. Bartnitzky & Speck-Hamdan, 2004) eine fachbezogene Konkretisierung dieser geben muss.
Die Leistungsfeststellung im Mathematikunterricht sollte demnach
-
kompetenzorientiert
-
kontinuierlich
-
prozessorientiert
-
transparent
-
informativ
-
differenziert
-
umfassend
erfolgen (vgl. Selter, 2006). Während eine solche Leistungsfeststellung vor allem dazu dient zu erfassen, an welcher Stelle sich das Kind in seinem individuellen Lernprozess befindet, geht es bei der Leistungsbeurteilung darum, diese Leistung an eine individuelle (personenbezogene) oder an eine anforderungsbezogene (zielbezogene) Bezugsnorm anzulehnen (vgl. Sacher, 2009, S. 87).
Die Leistungsbeurteilung sollte sich dabei stets an fachspezifischen Beurteilungskriterien orientieren. Im Lehrplan Mathematik für das Land NRW werden die folgenden Kriterien genannt, die zu einer umfassenden Leistungsbeurteilung führen sollten:
-
„Verständnis von mathematischen Begriffen und Operationen
-
Schnelligkeit im Abrufen von Kenntnissen
-
Sicherheit im Ausführen von Fertigkeiten
-
Richtigkeit bzw. Angemessenheit von Ergebnissen bzw. Teilergebnissen
-
Flexibilität und Problemangemessenheit des Vorgehens
-
Fähigkeit zur Nutzung vorhandenen Wissens und Könnens in ungewohnten Situationen
-
Selbstständigkeit und Originalität der Vorgehensweisen
-
Fähigkeiten zum Anwenden von Mathematik bei lebensweltlichen Aufgabenstellungen
-
Schlüssigkeit der Lösungswege und Überlegungen
-
mündliche und schriftliche Darstellungsfähigkeit
-
Ausdauer beim Bearbeiten mathematischer Fragestellungen
-
Fähigkeit zur Kooperation bei der Lösung mathematischer Aufgaben“
(MSW NRW, 2008, S. 67)
Hier wird deutlich, dass es im Mathematikunterricht der Grundschule nicht nur darum gehen kann, Kinder nur danach zu bewerten, ob Ergebnisse richtig oder falsch sind (PIKAS: Das zählt in Mathe). Vielmehr ist es wichtig, insbesondere auch solche Beurteilungskriterien zu berücksichtigen, die in mehr als nur Fehlerzahl und Reproduktion von Gelerntem Einsicht geben (vgl. Sundermann & Selter, 2006, S. 106f.).
Das bedeutet, dass die Lernenden informative, offene und prozessbezogene Aufgaben erhalten müssen, die sowohl die inhalts-, als auch die prozessbezogenen Kompetenzen gleichermaßen beinhalten, um die Vielfalt an Beurteilungskriterien berücksichtigen zu können.
Dabei ist es wichtig auch den Kindern und den Eltern die greifenden Beurteilungskriterien, die zum einen aufgabenunspezifisch, als auch aufgabenspezifisch sein können (vgl. KIRA: Prozessbezogene Kompetenzen beurteilen), bewusst zu machen und zu verdeutlichen, dass neben den richtigen Ergebnissen auch beispielsweise die Kreativität des Lösungswegs, die verständliche Darstellung des eigenen Vorgehens und der Umgang mit einem mathematischen Problem bewertet werden.
Sowohl bei den inhalts- als auch bei den prozessbezogenen Kompetenzen werden die Beurteilungskriterien mit Blick auf die Kompetenzerwartungen beschrieben. Für das Darstellen bedeutet dies beispielsweise, dass die Lehrkraft folgende Beurteilungskriterien heranziehen könnte:
-
Inwieweit wird die Darstellung passend zur Aufgabe (zum Problem) eingesetzt?
-
In welcher Form werden Darstellungen sicher und verständnisbasiert genutzt?
-
Wird sicher zwischen verschiedenen Repräsentationsebenen gewechselt (Handlung, Bild, Symbol, Sprache)?
-
Inwieweit wird Fachsprache zur Beschreibung einzelner Darstellungen genutzt?
-
Werden Darstellungen anderer erkannt bzw. verständlich erklärt?
-
Inwieweit werden eigene und fremde Darstellungen zueinander in Beziehung gesetzt?
Die oben genannten Beurteilungskriterien wurden aufgabenunspezifisch formuliert und können auf vielfältige Problemstellungen und Darstellungsweisen übertragen werden.
das Bild bekommt einen Fokus durch den grünen Bereich, sollte dieser nicht besser transparent sein?
Zur Beurteilung der Beispiellösungen zu der Aufgabe verschiedene Multiplikationsaufgaben mit dem Ergebnis 12 mit einem Zahlenstrahl darzustellen, können einige der oben genannten Beurteilungskriterien genutzt werden:
-
Inwieweit wird die Darstellung der Sprünge (Anzahl und Länge) auf dem Zahlenstrahl vom Kind passend zur jeweiligen Aufgabe eingesetzt?
-
Nutzt das Kind die Darstellung einer Multiplikationsaufgabe mit dem Zahlenstrahl sicher und verständnisbasiert?
-
Wechselt das Kind sicher zwischen Bild, Symbol und Sprache (mündlich und/oder schriftlich)?
-
Inwieweit nutzt das Kind Fachsprache zur Erklärung eigener oder fremder Darstellungen?
-
Inwieweit setzt das Kind eigene Darstellungen zueinander in Beziehung?
Derartige Beurteilungskriterien lassen sich in Anlehnung an die Kompetenzerwartungen für alle prozessbezogenen Kompetenzen formulieren und bilden so eine gute Basis für eine kompetenzorientierte, transparente, umfassende, informative, differenzierte Leistungsbewertung.
Hier wird deutlich, dass eine nicht rein an Ergebnissen orientierte Leistungsbewertung ein umfassendes Leistungskonzept (PIKAS: Plakate) benötigt. D. h. schriftliche Arbeiten müssen Entdeckungen und Begründungen zulassen, vor allem im Anfangsunterricht werden vielfältige Sprachanlässe benötigt, in denen die Lehrkraft einzelne Kinder beobachten kann und eine prozessorientierte Leistungsbewertung muss den Kindern die Möglichkeit geben den eigenen Lernprozess und den eigenen Lernfortschritt transparent vor Augen zu haben. Diagnosegespräche, Diagnoseaufgaben, Standortbestimmungen, Mathebriefe, Lerntexte, Beobachtungsbögen, Expertenarbeiten, Mathekonferenzen, u.a. bieten hier vielfältige Möglichkeiten zur Leistungsfeststellung, Leistungsbeurteilung und Leistungsrückmeldung. In Haus 9 und Haus 10 von PIKAS finden sie ausführliche Informationen zu diesen genannten Beispielen.
Weitere Informationen zum Thema Leistungsfeststellung und Leistungsbeurteilung finden Sie unter:
-
PIKAS: Haus 9
-
PIKAS: Haus 10
-
PIKAS: Das zählt in Mathe
-
PIKAS: Leistungskonzept
-
KIRA: Beurteilungskonzept
Um sich ggf. mit dem eigenen Kollegium auf den Weg zu machen die prozessbezogenen Kompetenzen noch einmal stärker in den Blick zu nehmen, bietet der Fortbildungsbaustein "Prozess- und inhaltsbezogene Kompetenzen fördern" in Haus 1 von PIKAS: Leitfaden für die Arbeit im Team Prozess- und inhaltsbezogene Kompetenzen eine grobe Übersicht zu den Inhalten und Zielen sowie einen detaillierten Leitfaden für die mögliche Arbeit im Team. Der Leitfaden führt durch aneinander anknüpfende Arbeitstreffen, die jeweils konkrete Arbeitsaufträge, Literaturverweise und PIKAS – Materialien bereithalten. Das Durchlaufen der einzelnen Arbeitstreffen ermöglicht die strukturierte Erarbeitung und die differenzierte Erschließung des ausgewählten Themenbereichs. Der Leitfaden kann flexibel genutzt werden und ist an persönliche Vorerfahrungen und die individuelle Lerngruppe anpassbar.
Den Leitfaden "Prozess- und inhaltsbezogene Kompetenzen fördern" für Lehrerteams finden sie hier:
-
PIKAS: Leitfaden prozess- und inhaltsbezogene Kompetenzen fördern