Basisinformationen
Entdeckendes Lernen und produktives Üben
Im Unterschied zum Lernen und Üben nach dem Prinzip der kleinen und kleinsten Schritte, bei dem "der Lernstoff in kleine 'Lernatome' zerlegt wird, die voneinander isoliert jeweils für sich durchgenommen werden" (Wittmann, 1994, S.159), sind die Inhalte beim Lernen und Üben im Sinne des Prinzips des aktiv-entdeckenden Lernens in größere Abschnitte mit Sinnzusammenhängen gegliedert.
Üben ist damit im Wesentlichen die Wiederaufnahme eines (entdeckenden) Lernprozesses, das Nocheinmalnachbilden, Nocheinmalnachbauen von Lernsituationen.
Winter, 1984, S.6
Lernen und Üben sind somit nicht voneinander zu trennen. Es wechseln sich immer wieder Phasen des "entdeckenden Übens" und "übenden Entdeckens" ab. Üben dient also nicht ausschließlich dem Auswendiglernen von Aufgabensätzen und Algorithmen. Vielmehr "sichert, vernetzt und vertieft [es] vorhandenes Wissen und Können [und] fördert die Einsicht in Gesetzmäßigkeiten und Beziehungen, die Phänomene aus der Welt der Zahlen, Formen und Größen strukturieren" (MSW NRW, 2008, S.55).
Die Kinder erarbeiten sich durch vielfältige Eigenaktivitäten Fertigkeiten und Wissen. Diese werden durch die Lehrkraft angeregt und unterstützt. Wie diese Unterstützung aussehen kann, zeigen wir an Beispielen in den PDF-Dokumenten auf.
Sinnzusammenhänge zwischen den einzelnen Lernabschnitten regen die Kinder an, ihre Lösungswege und -strategien im Hinblick auf die Anforderungen der Aufgabe zu entwickeln. Im Verlauf des Lern- und Übungsprozesses stoßen die Lernenden immer wieder auf Hürden und Schwierigkeiten. An diesen Stellen ist meist eine Anpassung der Lösungsstrategie notwendig, die entweder von den Lernenden selbstständig eingeschlagen oder von der Lehrkraft durch Tippkarten oder Impulse angeregt wird.
Diese Anpassungen der Strategien gehören, ebenso wie Fehler, zum Lernprozess dazu und sind wichtig für einen nachhaltigen Lernerfolg, der die Kinder dazu befähigt, erworbenes Wissen in verschiedenen Zusammenhängen anwenden und nicht nur Wissen in gleichartigen Aufgaben reproduzieren zu können.
Damit dies gelingen kann, bedarf es eines vielfältigen Aufgabenangebots mit verschiedenen Übungsformen.
Die Aufgabentypen können nach dem Grad der Strukturierung und nach der Darstellungsform unterschieden werden (Wittmann, 1999, S. 179).
Grad der Strukturierung
Beim unstrukturierten Üben sind die Aufgaben einer Übungsserie willkürlich ausgewählt. Jede Aufgabe wird isoliert für sich betrachtet und gelöst. Beispiele hierfür sind Aufgabenpäckchen ohne Zusammenhang zwischen den Aufgaben eines Päckchens oder Wimmelbilder zu denen passende Rechenaufgaben gefunden werden sollen (siehe Übungsmatrix weiter unten).
Weisen die Aufgaben einen ganzheitlichen Strukturzusammenhang auf, so handelt es sich um strukturiertes Üben. Dadurch können die Aufgaben mit Hilfe der Struktur gelöst und korrigiert werden. Beispiele hierfür sind Entdeckerpäckchen oder Zahlenketten (siehe Übungsmatrix weiter unten). Die Übergänge zwischen unstrukturierten und strukturierten Aufgabenserien sind fließend. So können Aufgaben von schwach bis stark strukturiert sein.
Darstellungsform
Beim gestützten Üben erfolgt die Bearbeitung der Aufgaben mit Hilfe von Darstellungen oder Handlungen am Material. Neben der Lösung können auch Erklärungen oder Begründungen durch Material veranschaulicht werden.
Erfolgt die Lösung der Aufgaben auf rein symbolischer Ebene, so handelt es sich um formales Üben (Wittmann, 1999, S.179)
ÜbungsMatrix
In der Übungsmatrix werden beide Kriterien kombiniert. So wird sichtbar, welche konkreten Aufgabentypen entsprechend des Konzepts des produktiven Übens im Unterrichtsverlauf berücksichtigt werden sollten. Der Fokus liegt insbesondere auf den strukturierten Aufgabentypen, welche die Einsicht in Zusammenhänge fördern.
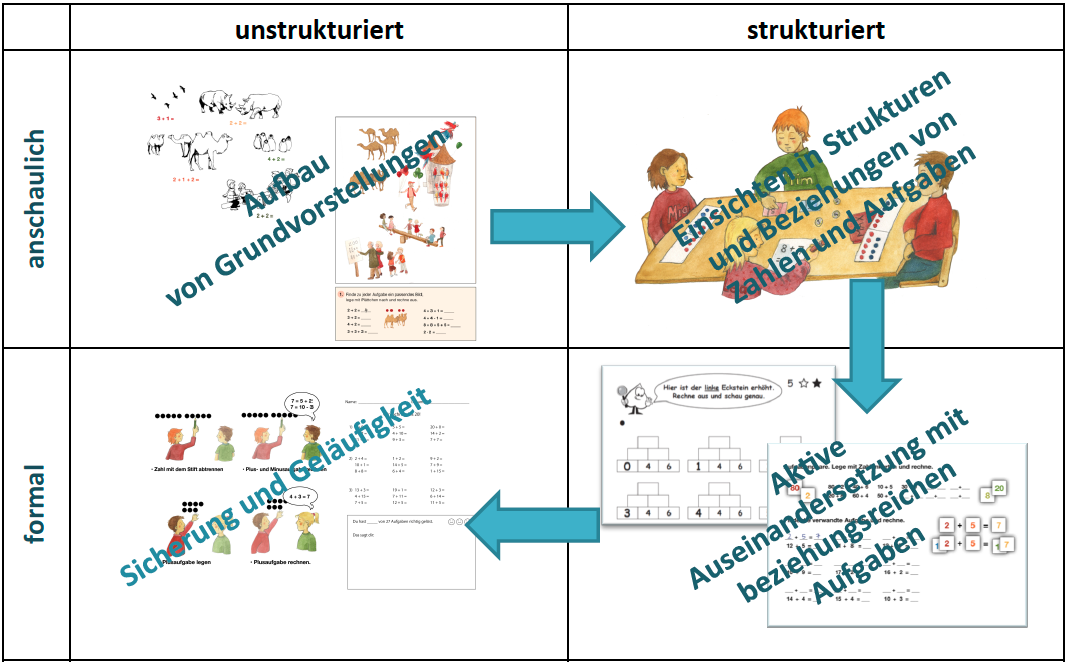primakom: Übungsmatrix aus der Präsentation "Üben im Mathematikunterricht"
(Wittmann, 1999, S.179)
Die einzelnen Aufgabentypen finden in der Regel zu unterschiedlichen Zeitpunkten im Lernprozess Beachtung.
Für den Aufbau von Grundvorstellungen sind Operationen an konkretem Material und bildlichen Darstellungen zentral. Aus diesem Grund bilden, im Sinne der fortschreitenden Schematisierung und des Vier-Phasen-Modells, gestützte Aufgabentypen den Ausgangspunkt des Lernens.
Auch wenn die Automatisierung von Aufgaben (z.B. Blitzrechnen) das Ziel des Lernprozesses ist, so darf nicht zu früh zum unstrukturiert formalen Üben übergegangen werden, damit die Kinder eine Verstehensgrundlage entwickeln können und ihr Wissen auf andere Sachverhalte übertragen können. Einer kalkülbasierten Lösung von Aufgaben soll damit entgegengewirkt werden (Wittmann, 1999, S.181).
Themenfelder der Dokumente
In den folgenden Dokumenten werden, unter Berücksichtigung der zentralen Aspekte der Subtraktion, drei verschiedene Aufgabenformate im Sinne des produktiven Übens sowie deren Umsetzung im Unterricht vorgestellt. Da produktive Übungsformate in allen Schuljahren eingesetzt werden können, sind die Ausführungen jeweils schwerpunktmäßig auf die Klasse 1, 2 oder 3/4 ausgerichtet.
Die Ausgangsaufgabe wird jeweils aus dem Blickwinkel der vier Schwerpunkte Prozessbezogene Kompetenzen ausbauen, Matheschwierigkeiten begegnen, Sprachbildend unterrichten und Mathestärken fördern betrachtet und anhand exemplarischer Unterrichtsanregungen für die Umsetzung im Unterricht konkretisiert.
Ausgangsaufgabe
Rechne aus und setze fort?
Was fällt dir auf? Erkläre.
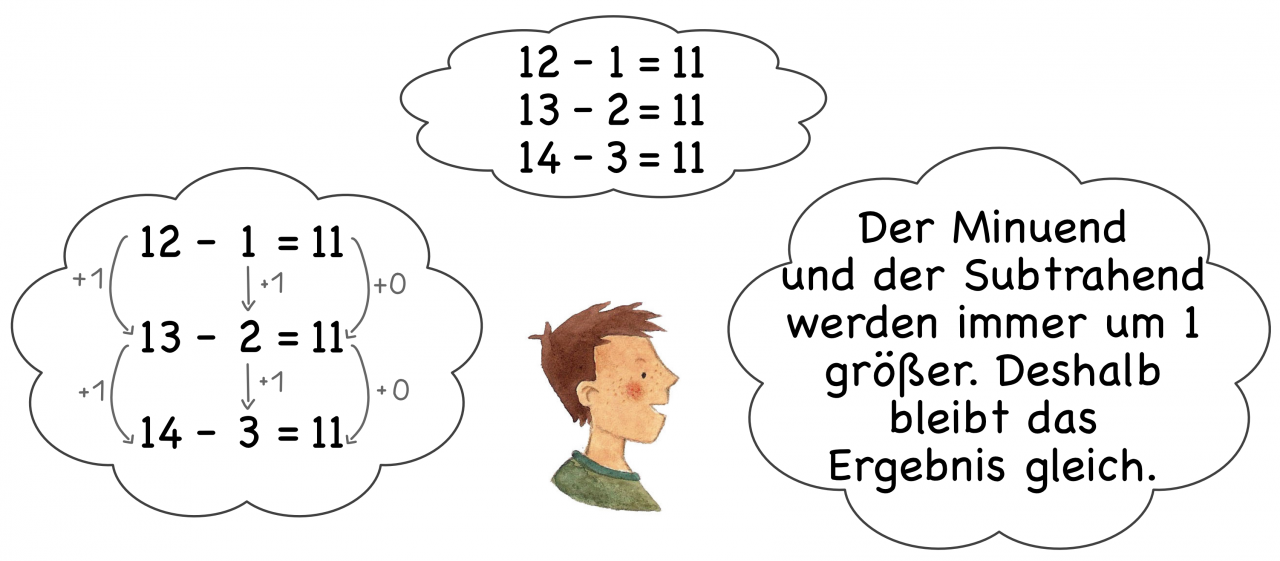
Entdeckerpäckchen sind ein weit verbreitetes Aufgabenformat und gehören zu den formal, strukturierten Übungsformaten. Die Aufgaben eines Päckchens sind durch operative Zusammenhänge, wie die konstante Erhöhung oder Erniedrigung des Minuenden oder des Subtrahenden oder durch die gleichsinnige Veränderung von Minuend und Subtrahend, strukturiert.
Ziel ist, dass die Kinder diese Zusammenhänge zwischen den einzelnen Aufgaben erkennen und zur Lösung nutzen. Weiterhin sollen die Kinder die Beziehungen zwischen den einzelnen Zahlen, den Ergebnissen und den Aufgaben beschreiben. Dabei können Veranschaulichungen helfen. Langfristig soll die Argumentationsfähigkeit der Kinder gefördert werden, indem die Entdeckungen zunehmend allgemeingültig erklärt werden können. Hierbei spielen Forschermittel eine zentrale Rolle.
Durch die Einsicht in die operativen Strukturen der einzelnen Entdeckerpäckchen können Zahl- und Operationsvorstellungen gefördert werden (Krauthausen, 2018, S.176 f.).
Indem Zahlenwerte und bzw. oder die Komplexität der operativen Veränderungen variiert werden, können alle Kinder einer Lerngruppe an einem gemeinsamen Lerngegenstand arbeiten, wodurch das Aufgabenformat auch für das jahrgangsübergreifende Lernen geeignet ist. Die Ausführungen im Folgenden fokussieren sich auf die Jahrgangsstufe 1, können jedoch an vielen Stellen für andere Jahrgangsstufen adaptiert werden.
Subtraktion produktiv üben - Entdeckerpäckchen
Ausgangsaufgabe
Bilde eine zweistellige Zahl. Subtrahiere erst die Einerziffer, dann die Zehnerziffer.
Was fällt dir auf? Erkläre.
Beim Übungsformat "Stellenwerte abziehen" wird eine zweistellige Zahl gebildet. Von dieser wird zunächst die Zehnerziffer abgezogen. Anschließend wird vom Ergebnis die Einerziffer subtrahiert. Als Ergebnis erhält man stets das Neunfache der Zehnerziffer.
Zwar ist durch die Bildungsregel der Aufgaben bereits eine Struktur gegeben, jedoch ist diese nicht so unmittelbar ersichtlich wie bei den Entdeckerpäckchen. Die Kinder müssen zunächst einige Aufgaben berechnen und die Ergebnisse miteinander vergleichen, um Zusammenhänge entdecken zu können. Eine weitere Voraussetzung ist die Einsicht in multiplikative Zusammenhänge, um aus den Ergebnissen Rückschlüsse auf die Aufgabenstruktur ziehen zu können.
Die Bearbeitung kann dennoch auf verschiedenen Anforderungsniveaus erfolgen. Neben der Bildung und Berechnung der Aufgaben, kann in einem ersten Schritt eine auf konkrete Beispiele bezogene Beschreibung der Auffälligkeiten erfolgen. Anschließend können diese Zusammenhänge beispielgebunden oder auch allgemeingültig erläutert werden.
Die Ausführungen im Folgenden fokussieren sich auf die Jahrgangsstufe 2.
Subtraktion produktiv üben - Stellenwerte abziehen
Ausgangsaufgabe
Bilde eine dreistellige Zahl und ihre Umkehrzahl. Subtrahiere die kleinere Zahl von der größeren Zahl.
Was fällt dir auf?
Beim Aufgabenformat Umkehrzahlen werden eine dreistellige Zahl und ihre Umkehrzahl gebildet. Die kleinere der beiden gebildeten Zahlen wird von der größeren subtrahiert. Als Ergebnis erhält man das 99-fache des Unterschieds der Hunderter- und Einerziffer.
Wie auch bei der Aufgabe "Stellenwerte abziehen" weisen die Aufgaben durch die Bildungsregel bereits eine Struktur auf. Durch die Bildung und Berechnung mehrerer Aufgaben können Zusammenhänge zwischen den Ergebnissen erkannt, beschrieben und begründet werden, wodurch eine Bearbeitung der Ausgangsaufgabe auf verschiedenen Anfordungsniveaus erfolgen kann.
Die Ausführungen im Folgenden fokussieren sich auf die Jahrgangsstufen 3 und 4, wobei diese Ausgangsaufgabe auch bereits in Klasse 2 mit zweistelligen Umkehrzahlen genutzt werden kann.
Subtraktion produktiv üben - Umkehrzahlen
Material und Informationen
Weiteres Material finden Sie auf den Partnerprojektseiten mit dem Materialfinder
Testen Sie Ihr Wissen zu dem Thema mit unserem Kira-Check
