Fehler gehören zum Lernprozess dazu und auch zwischenzeitliche Schwierigkeiten in einzelnen mathematischen Bereichen treten in mancher Lernbiographie auf, ohne dass direkt von Rechenschwierigkeiten gesprochen werden müsste.
Die Lernenden aber, die umfangreichere Probleme haben, mathematische Inhalte zu verstehen und deren Schwierigkeiten grundlegend sind und sich erheblich auf das mathematische Verständnis auswirken, sollten möglichst frühzeitig wahrgenommen und entsprechend unterstützt werden. In der Literatur sind für diese „besonderen Schwierigkeiten beim Rechnen“ unterschiedliche Begrifflichkeiten zu finden, jedoch keine allgemein anerkannte Definition und auch kein allgemein anerkanntes Diagnoseverfahren. Allerdings lassen sich vier zentrale Merkmale (vgl. Schipper 2011 und Wartha & Schulz, 2014) identifizieren, die auf Rechenschwierigkeiten hindeuten:
-
Nicht tragfähiges Zahlverständnis
-
Nicht tragfähiges Operationsverständnis
-
Nicht tragfähiges Stellenwertverständnis
-
Verfestigung des zählenden Rechnens
Eins der vier Schwerpunktthemen von PIKAS kompakt widmet sich explizit dem Thema Matheschwierigkeiten begegnen und stellt wesentliche theoretische Grundlagen kompakt zusammen und verweist auf weiterführende Informationen und Materialien.
Zudem werden in den sechs Themenhäusern exemplarisch Unterrichtsanregungen unter besonderer Berücksichtigung matheschwacher Kinder dargestellt, indem ausgehend von einer Ausgangsaufgabe zunächst aufgezeigt wird, welche Besonderheiten oder Stolpersteine es bei dem Thema zu beachten gilt. Entsprechend werden jeweils unterrichtspraktische Impulse, Aufgaben und Materialanregungen für den Unterricht aufgeführt.
Um ebenfalls mathematische Schwierigkeiten zu berücksichtigen, die sich nicht nur auf den arithmetischen Bereich beziehen, sondern bspw. auch auf geometrische Fähigkeiten, Größenvorstellungen usw., wird auf PIKAS kompakt der Begriff Rechenschwierigkeiten auf Matheschwierigkeiten ausgeweitet.
Weitere Informationen zum Thema Rechenschwierigkeiten finden Sie unter
-
PIKAS: Fachoffensive - Handreichung Rechenschwierigkeiten
-
PIKAS: Fortbildung - Basiskompetenzen sichern - Rechenschwierigkeiten vermeiden
-
PIKAS: Selbststudium - Basiskompetenzen sichern - Rechenschwierigkeiten vermeiden
-
Mathe inklusiv: Inhalte
Eine wesentliche Aufgabe des Mathematikunterrichts in der Grundschule stellt die Entwicklung eines tragfähigen Zahlverständnisses dar. Demnach sollen Kinder Zahlen nicht nur als Zahlsymbole wahrnehmen, sondern umfangreiche Vorstellungen zu diesen aufbauen, die sie im Laufe der Zeit flexibel abrufen können.
Wie heißt die Zahl? Wie sieht sie aus? Wie lässt sie sich unterschiedlich darstellen?
Wo befindet sie sich in der Zahlenreihe? Welche Nachbarzahlen hat sie?
In welcher Beziehung steht die Zahl zu anderen Zahlen?
In welche Zahlen lässt sich die Zahl zerlegen?
wieso ist der Text petrol, fett und zentriert?
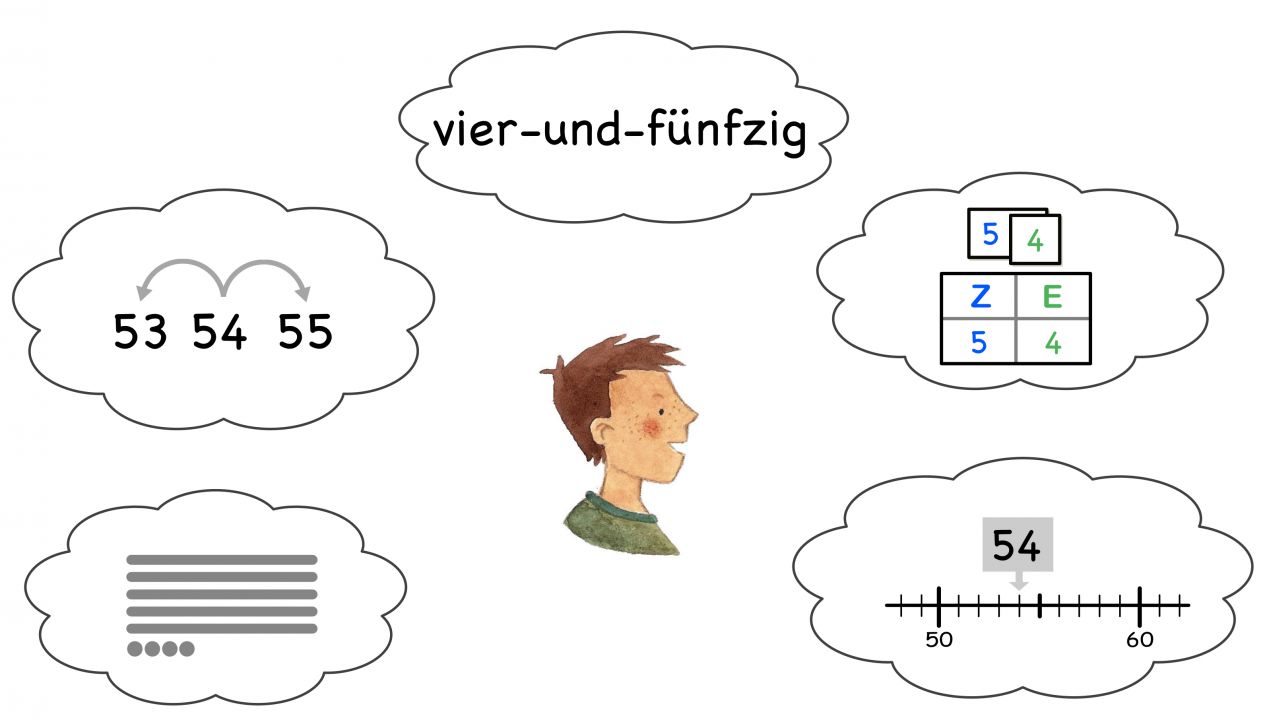
Die Entwicklung eines tragfähigen Zahlverständnisses sowie die Einsicht in Zahlbeziehungen und unser Stellenwertsystem beginnen bereits grundlegend im Anfangsunterricht, so dass die Vorstellungen bei der Erweiterung des Zahlenraums aufgegriffen und strukturgleich weiterentwickelt werden. Folglich ist ein frühzeitiger Aufbau des Zahlverständnisses bedeutsam für die Prävention von Matheschwierigkeiten. Bereits im Anfangsunterricht sollten daher die individuellen Vorkenntnisse der Kinder im Zahlenraum bis 10 bzw. bis 20 berücksichtigt werden, um durch geeignete Förderanregungen das Zahlverständnis ausweiten zu können. Um jedoch Zahlen mit vielfältigen Bedeutungen verknüpfen zu können, muss der Unterricht ausreichend Gelegenheiten bieten, ein umfangreiches Zahlverständnis zu entwickeln.
Für die Unterrichtsgestaltung bedeutet dies, ähnlich zur Förderung des Operationsverständnisses, dass Kinder:

Weitere Informationen zum Thema Zahlverständnis finden Sie unter
-
PIKAS: Fortbildung - Basiskompetenzen sichern - Rechenschwierigkeiten vermieden - Zahlverständnis
-
PIKAS: Unterricht - Schulanfang Arithmetik in der Schuleingangsphase
-
Mathe inklusiv: Inhalte - Zahlvorstellungen
-
primakom: Inhalte - Zahlen und Operationen - Zahlverständnis
-
Mathe sicher können primar: Natürliche Zahlen - Zahlverständnis
Die Entwicklung eines sicheren Stellenwertverständnisses bildet die Grundlage für erfolgreiches Mathematiklernen. Es ist zentral, um insbesondere Zahlen und Rechnungen verstehen zu können. Allerdings bedarf die Entwicklung von Stellenwertverständnis einer geeigneten Unterstützung, die bereits mit Eintritt in die Schuleingangsphase beginnt. Die folgenden drei grundlegenden Prinzipien (Wartha & Schulz, 2014, S. 48ff.) sind zentral für die Entwicklung des Stellenwertverständnisses:
Jeweils 10 Objekte einer Bündelungseinheit können zu einem 10er-Bündel zusammengefasst und anschließend in ein Objekt der nächst höheren Stellenwert eingetauscht werden.
Die einzelnen Ziffern eines Zahlzeichens haben abhängig von ihrer Position innerhalb der Zahl bzw. in der Stellenwerttafel einen unterschiedlichen Wert. Eine 5 an der Zehnerstelle bedeutet fünf Zehner. Eine 5 an der Einerstelle bedeutet fünf Einer. Veranschaulichen lässt sich das Prinzip des Stellenwertes mithilfe des strukturierten Würfelmaterials sowie der Stellenwerttafel.
Der Wert der Ziffer an einer bestimmten Position innerhalb der Zahl bzw. in der Stellenwerttafel gibt die Anzahl der entsprechenden Bündel des Stellenwertes an. Eine 4 an der Einerstelle bedeutet vier Einer. Eine 5 an der Einerstelle bedeutet fünf Einer.
Ein Stolperstein auf dem Weg zu einem sicheren Stellenwertverständnis ergibt sich aus der Schreib- und Sprechweise der Zahlen in der deutschen Sprache. Zum einen werden die meisten Zahlworte invers gesprochen, d. h. die Sprechweise weicht von der Notation der Zahlen ab (bspw. gesprochen: vier-und-fünfzig, aber 54 geschrieben), zum anderen werden manche Zahlen unregelmäßig gebildet (bpspw. elf, zwölf, drei-zehn, vier-zehn). Um Schwierigkeiten bei der Bildung von Zahlworten und der Notation von Zahlen zu begegnen, ist es daher besonders wichtig, dass die Lernenden materialgestützt sowie sprachlich unterstützt Einsicht in das dekadische Zahlsystem entwickeln.
 Bildunterschrift
Bildunterschrift
Weitere Informationen zum Thema Stellenwertverständnis finden Sie unter
-
PIKAS: Fortbildung: Basiskompetenzen sichern - Rechenschwierigkeiten vermeiden - Stellenwertverständnis
-
primakom: Inhalte - Stellenwertverständnis
-
Mathe sicher können Primar: Natürliche Zahlen - Zahlverständnis - Bausteine N1 und N01 Stellenwerte verstehen
-
KIRA: Arithmetik - Zahlverständnis - Stellenwertverständnis
Während es bei der Entwicklung des Zahlverständnisses darum geht, die Bedeutung der Zahlen zu verstehen, Zahlen zu vergleichen und zu zerlegen sowie Zahlen in Beziehung zueinander zu erkennen, liegt bei der Entwicklung des Operationsverständnisses der Fokus darauf, die vier Grundrechenoperationen zu verstehen und diese mit Bedeutungen zu verknüpfen.
wieso ist der Text fett, zentriert und petrol?
Was bedeutet eigentlich multiplizieren?
Welche Handlungen können sich hinter dem Malzeichen verbergen?
Was passiert mit den Zahlen, wenn man sie multipliziert?
Um ein tragfähiges Operationsverständnis zu entwickeln und dieses flexibel abrufen zu können, sollen Lernende im Unterricht ausreichend Gelegenheiten bekommen, Vorstellungsbilder (materialgestützt) aufzubauen. Am Beispiel der Multiplikation zeigt die Grafik, wie die Schülerin die formale Malaufgabe mit (Handlungs-)Erfahrungen verknüpft.

Die Kinder bauen so im Laufe der Zeit ein Repertoire an Vorstellungsbildern auf, welches es ihnen ermöglicht, multiplikative Strukturen in unterschiedlichen Situationen und in verschiedenen Darstellungsformen zu erkennen und auf andere Situationen zu übertragen.
Zentral ist, dass Kinder ausreichend Gelegenheiten bekommen, diese Vorstellungen zu entwickeln. Folgende drei Aspekte sollten daher bei der Unterrichtsplanung, analog zum Aufbau des Zahlverständnisses, Berücksichtigung finden:

Damit Kinder nicht nur die formalen Rechenzeichen sehen, sondern die Bedeutung hinter der Rechenoperation verstehen und begründet entscheiden können, wann sie minus, plus, mal oder geteilt rechnen, ist es wichtig, die Grundvorstellungen zu den vier Rechenoperationen zu thematisiert. Die Grafik veranschaulicht bspw. die drei Grundvorstellungen Abziehen, Vergleichen und Ergänzen der Subtraktion.
das Bild ist nicht freigestellt
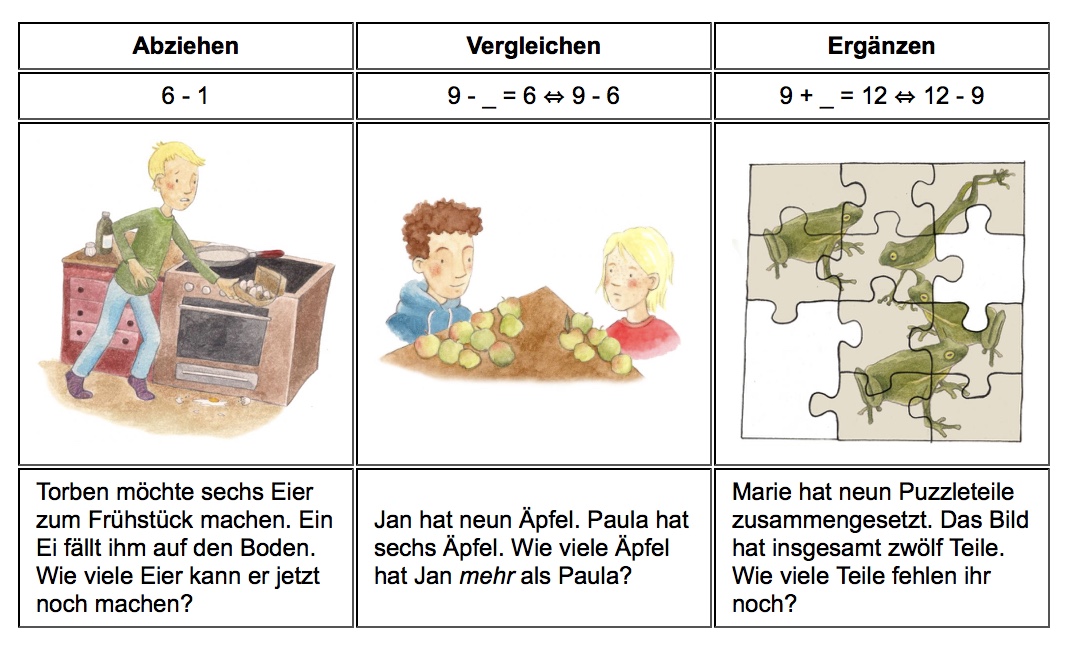 Quelle: primakom: Inhalte - Operationsverständnis
Quelle: primakom: Inhalte - Operationsverständnis
Zudem ist es wichtig, dass Lernende unterschiedliche Darstellungsformen (Material, Bild, Sprache und Mathesprache) kennenlernen und Übertragungen von einer in andere Darstellungsformen regelmäßig nachvollziehen, selbst durchführen sowie sprachlich begründen. Die Übung zum flexiblen Darstellungswechsel unterstützen die Kinder beispielsweise darin, eine Rechenoperationen in der Darstellung eines Bildes oder einer Sachaufgabe zu erkennen oder umgekehrt, einen Term in eine andere Darstellungsform zu übersetzen und z. B. eine eigene Sachaufgabe zu formulieren.
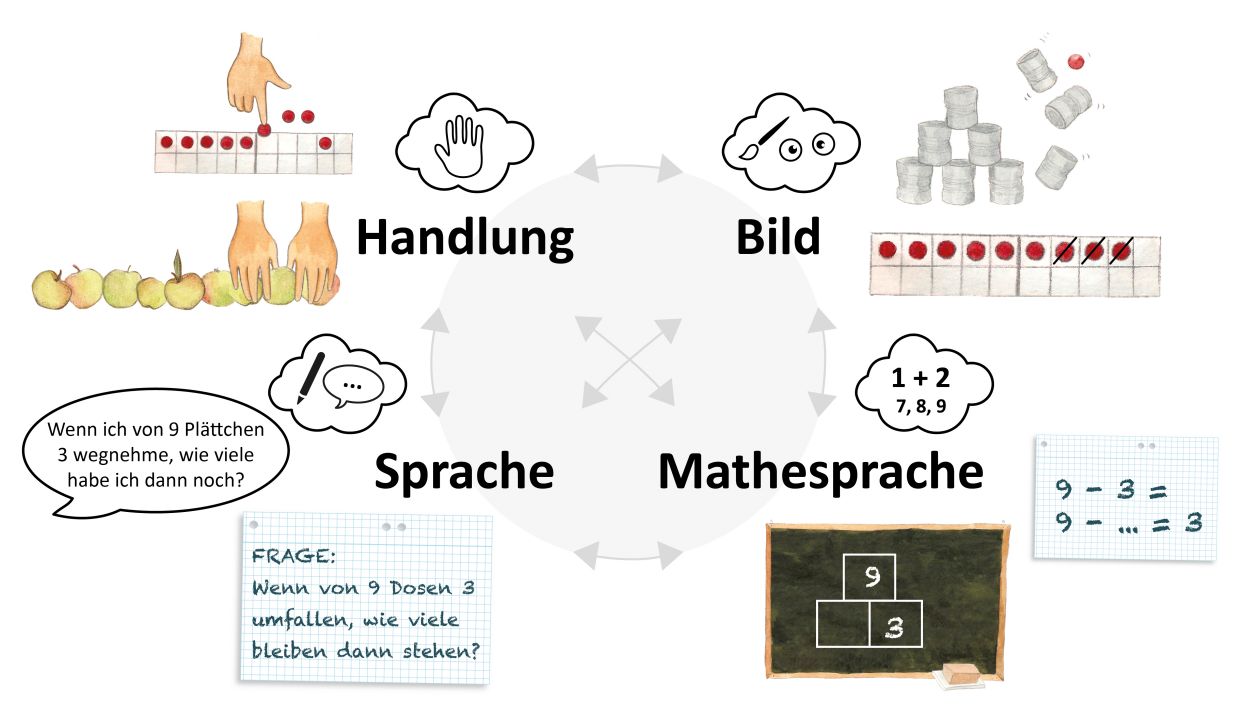
Der Ausbau des Operationsverständnisses im Sinne des Blickes für Strukturen und Beziehungen zwischen Aufgaben (z. B. Nachbaraufgaben wie 6+7, 6+6, 5+6) sowie zwischen Rechenoperationen (z. B. Umkehroperationen wie 20 : 5 = 4, denn 4 · 5 = 20) befähigt die Kinder zum flexiblen und sicheren Rechnen, indem sie bereits bekannte Aufgaben zur Lösung anderer Aufgaben heranziehen.
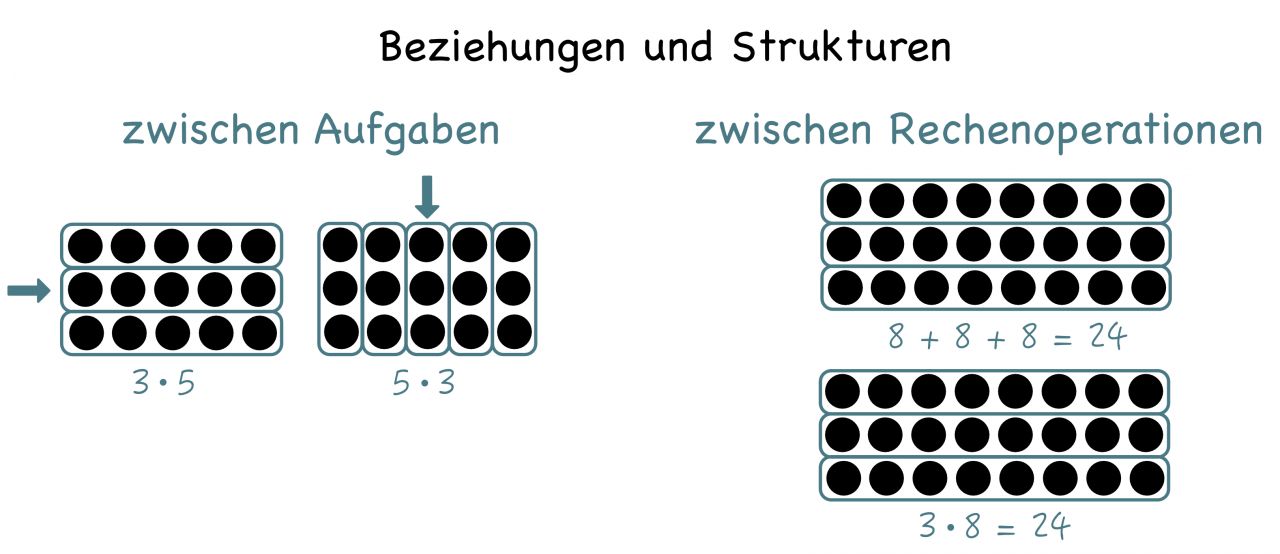
Weitere Informationen zum Thema Operationsverständnis finden Sie unter
-
PIKAS: Unterricht - Zahlen und Operationen - Darstellungsmittel
-
PIKAS: Fortbildung - Basiskompetenzen sichern - Rechenschwierigkeiten vermeiden - Operationsverständnis
-
primakom: Inhalte - Zahlen und Operationen - Operationsverständnis
-
KIRA: Arithmetik - Zahlverständnis - Bildliche Darstellung
-
Mathe sicher können primar: Natürliche Zahlen - Operationsverständnis - Baustein N3 Addition und Subtraktion verstehen; N4 Multiplikation und Division verstehen
Zu Beginn der Grundschulzeit stellt das zählende Rechnen ein häufig genutztes und auch zielführendes Vorgehen beim Lösen von Addition- und Subtraktionsaufgaben dar. Vergrößert sich allerdings der Zahlenraum, stößt das zählende Vorgehen an seine Grenzen, da es zeit- sowie konzentrationsaufwändig und zudem fehleranfällig ist. Allmählich sollte dieses daher durch effektivere Vorgehensweisen abgelöst werden. Erfolgt diese Ablösung nicht, so zählt die Verfestigung des zählenden Rechnens als deutliches Merkmal für Rechenschwierigkeiten. Daher gilt es, die Vorgehensweisen der Kinder sensibel wahrzunehmen und die Ablösung vom zählenden Rechnen anzuregen.
Im Unterricht sollen dazu strukturierte Materialien eingesetzt werden, die nicht-zählende Strategien ermöglichen. Zudem ist es erforderlich, den Kindern Gelegenheit zu bieten, verschiedene Rechenwege kennenzulernen, sich darüber auszutauschen sowie mathematische Gespräche über geschickte Lösungswege zu führen. Des Weiteren gilt es Entdeckeraufgaben in den Unterricht zu integrieren, so dass gezielt Beziehungen zwischen Aufgaben in den Blick genommen werden können und ein Austausch darüber entsteht, wie diese zum Lösen verwandter Aufgaben genutzt werden können.
Weitere Informationen zum Thema Nicht-zählendes Rechnen finden Sie unter
-
PIKAS: Unterricht - Zahlen und Operationen - Zahlraum bis 20 - Sicher im 1+1
-
PIKAS: Unterricht - Zahlen und Operationen - Zahlraum bis 20 - Sicher im 1-1
-
PIKAS: Fortbildung - Basiskompetenzen sichern - Rechenschwierigkeiten vermeiden - Nicht zählendes Rechnen: 1+1 und 1-1
-
PIKAS: Fortbildung - Basiskompetenzen sichern - Rechenschwierigkeiten vermeiden - Nicht zählendes Rechnen: 1∙1 und 1:1
-
primakom: Inhalte - Zahlen und Operationen - Kopfrechnen
-
primakom: Inhalte - Zahlen und Operationen - Nicht zählendes Rechnen
Kinder sollen Gelegenheit bekommen, aus ihren Fehlern zu lernen. Diesbezüglich stellt die individuelle Förderung eine bedeutende Chance für Lernende dar, aber auch eine große Herausforderung für Lehrkräfte: Diese sollen gute Förderaktivitäten bereitstellen, die möglichst an den individuellen Lernständen der Kinder anknüpfen und sie beim
(Weiter-)Lernen entsprechend unterstützen. Gleichzeitig dürfen die zeitlichen und materiellen Ressourcen aber nicht aus dem Blick verloren werden. Gewisse Rahmenbedingungen, insbesondere eine fehlerfreundliche Grundhaltung, bilden die Basis für eine gute und auch praktikable Förderung:
-
Eine fehlerfreundliche Lernatmosphäre – den Kindern vermitteln, dass Fehler gemacht werden "dürfen" und Fehlermachen zum Lernen dazugehört
-
Ein stärkenorientierter Blick – hinter Fehlern stecken meist durchaus sinnvolle Überlegungen, auf denen aufgebaut werden kann
-
Wissen um typische Fehlertypen – bestimmten Fehler sind systematisch, hinter ihnen stecken fehlerhafte Vorstellungen
-
Ein produktiver Umgang mit Fehlern – Fehler werden als Lerngelegenheiten, als Ausgangspunkt zum Weiterdenken und Lernen genutzt
-
Kommunikationsfördernde Situationen – Fehler werden nicht tabuisiert, sondern thematisiert, so dass gemeinsam über Fehler gesprochen und nachgedacht werden kann
-
Diagnosegeleitete Förderung – es gilt wahrzunehmen, welche Fehler auftreten, woraus diese resultieren und entsprechend passende Förderaktivitäten anzubieten
-
Verstehensorientiertes Lernen – Aufgaben und Materialien orientieren sich an einem fundierten Aufbau von Verständnis und inhaltlichen Vorstellungen (vgl. Hußmann, Nührenbörger, Prediger & Selter, 2014)
wieso hat das Bild einen grauen Hintergrund?
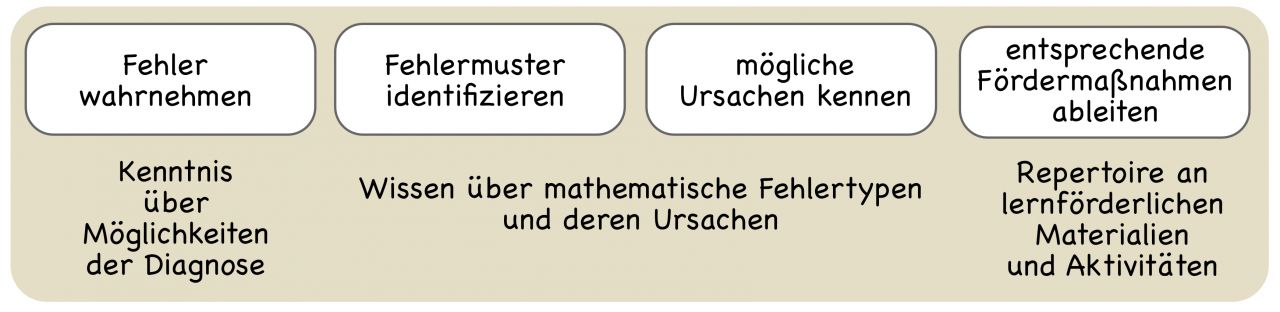
Wichtig ist vor allem die Verknüpfung von Diagnose und Förderung. Die Lehrperson muss diagnostizieren, wo die Schwierigkeiten und auch Fähigkeiten liegen und entscheiden, wie entsprechend gefördert werden kann. Diagnostische Situationen bspw. in Form informativer Aufgaben (KIRA: Informative Aufgaben), mündlich oder schriftlich, geben Aufschluss über die Denkwege der Kinder und bieten eine gute Grundlage für eine diagnosegeleitete Förderung.
Weitere Informationen zum Thema Diagnosegeleitete Förderung finden Sie unter
-
PIKAS: Fortbildung - Beurteilen und Rückmelden - Leistungen feststellen
-
PIKAS: Fortbildung - Lernstände wahrnehmen
-
Mathe inklusiv: Leitideen - Diagnosegeleitet fördern
-
primakom: Grundlagen - Kinder denken anders - Fehler
-
KIRA: Diagnose: Informative Aufgaben
Testen Sie Ihr Wissen zu dem Thema mit unserem Kira-Check