Basisinformationen
Die Entwicklung tragfähiger Zahlvorstellungen ist ein zentrales Ziel des Mathematikunterrichts und stellt die Grundlage für die weitere mathematische Entwicklung dar (Krauthausen & Scherer, 2014).
Für den Erwerb gesicherter Zahlvorstellungen sind folgende Elemente grundlegend:
Wesentlich für den Erwerb tragfähiger Grundvorstellungen sind der Aufbau und die Festigung des kardinalen und ordinalen Zahlverständnisses sowie des Stellenwertverständnisses.
Der kardinale Zahlaspekt beschreibt die Erfassung von Zahlen als Anzahlen von Objekten einer Menge. Durch die Verwendung strukturierter Darstellungen (z. B. Zwanziger-Feld) können die Lernenden die Anzahlen der Objekte nicht nur durch reines Auszählen, sondern auch quasi-simultan mit Hilfe der Fünfer- und Zehner-Struktur ermitteln.
Der ordinale Zahlaspekt beschreibt die Folge der natürlichen Zahlen und entsprechende lineare Darstellungen (z. B. Zwanzigerkette, Zahlenstrahl). Jedem Objekt wird beim Zählen genau ein Zahlwort zugeordnet, worduch Rangplätze ermittelt werden können. Voraussetzung hierfür ist die gesicherte Kenntnis der Zahlwortreihe (Selter & Zannetin, 2018; Krauthausen, 2018; Schipper, 2009).
Ein gesichertes Stellenwertverständnis impliziert die Beherrschung der Stellenwertschreibweise und der dezimalen Bündelung. Bündelungseinheiten des dezimalen Stellenwertsystems sind Zehnerpotenzen. Dies bedeutet, dass "jeweils zehn Einheiten einer kleineren Einheit zu genau einer Einheit der nächst größeren zusammengefasst (werden können)" (Mosandl & Nührenbörger, 2014, S. 21). Dadurch hat jede Ziffer innerhalb der Zahl einen festgelegten Wert.
Die Fähigkeit zum Darstellungswechsel ist wesentlich für die flexible Nutzung der unterschiedlichen Darstellungsformen von Zahlen:
Handlungen mit Material, Bilder, gesprochene oder geschriebene Sprache und symbolische Darstellungen (Mathesprache). Für den Aufbau und die Festigung von Zahlvorstellungen im Anfangsunterricht sind bildliche Darstellungen und Handlungen mit Material von besonderer Bedeutung, da sie an die Alltagserfahrungen der Kinder anknüpfen und diese aufgreifen. Durch die Vernetzung der Darstellungsformen kann eine Verständnisgrundlage für die Nutzung der mathematischen Symbole geschaffen werden, weshalb alle Darstellungsformen im Lernprozess immer wieder zum Tragen kommen sollen (Kuhnke, 2012).
Die Nutzung von Zahlbeziehungen ist eine zenztrale Voraussetzung für die Entwicklung und Nutzung flexibler Rechenstrategien, denn jede Zahl steht als Vorgänger, Nachfolger oder Vielfaches in Beziehung zu anderen Zahlen und kann zerlegt werden. Diese Teil-Teil-Ganzes-Beziehungen gilt es in einem verständnisbasierten Mathematikunterricht herauszuarbeiten und für flexible mentale Zahlvorstellungen sowie zur Nutzung flexibler Rechenstrategien nutzbar zu machen (Gerster & Schultz, 2004; Gaidoschik, 2010).
Unter Berücksichtigung der Aspekte "Grundvorstellungen entwickeln, Darstellungen vernetzen und Zahlbeziehungen nutzen" können im Anfangsunterricht durch verschiedene Aufgabenformate und Zahldarstellungen die Kinder dazu angeregt werden, ein umfassendes Zahlverständnis zu entwickeln.
Für den Anfangunterricht werden die folgenden zentralen Aspekte dargestellt:
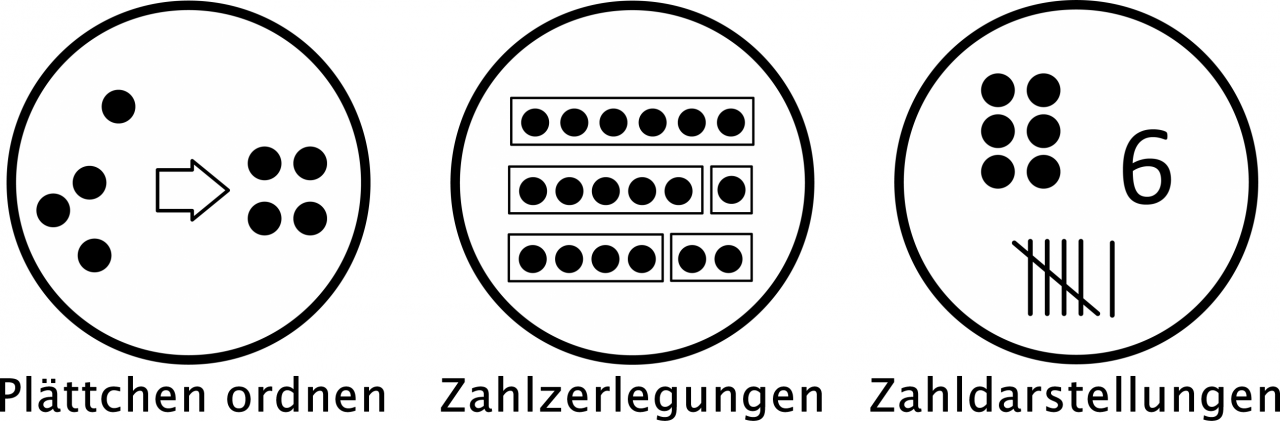
In den nun folgenden Dokumenten werden diese zentralen Aspekte des Anfangsunterrichts jeweils am Beispiel einer Ausgangsaufgabe unter den vier Schwerpunktthemen prozessbezogene Kompetenzen ausbauen, Matheschwierigkeiten begegnen, sprachbildend unterrichten und Mathestärken fördern betrachtet und anhand exemplarischer Unterrichtsanregungen für die Umsetzung im Anfangsunterricht konkretisiert.
Ausgangsaufgabe
Nimm Plättchen und ordne sie.
Ein anderes Kind soll schnell erkennen können, wie viele es sind.
Plättchen sind ein zentrales Anschauungs- und Handlungsmaterial im Anfangsunterricht, da sie leicht handhabbar und zur Dokumentation von Arbeitsergebnissen gut von den Kindern gezeichnet werden können. Des Weiteren werden im Verlauf der gesamten Grundschulzeit Punktefelder (Zwanziger- und Hunderterpunktefeld, Tausenderbuch) zur Förderung des kardinalen Zahlaspekts genutzt, die eine Abstraktion der Handlung mit Plättchen darstellen.
Ziel des Anfangsunterrichts ist die simultane beziehungsweise quasi-simultane Erfassung von Anzahlen einer Menge an Objekten. Anzahlen bis vier oder fünf können von den meisten Kinder bei der Einschulung auf einen Blick, also simultan erfasst werden (Padberg & Benz, 2011, S. 17).
Durch Anordnung der Plättchen, beispielsweise in Zehnerreihen oder Gruppen mit immer fünf oder zehn Plättchen, kann auch die Anzahl an Objekten größerer Mengen quasi-simultan, also auf den zweiten Blick, durch Ausnutzung der Strukturierung ermittelt werden. Grundsätzlich ist das Abzählen von Objekten im Anfangsunterricht auch eine Möglichkeit zur Anzahlerfassung und in einem ersten Schritt notwendig zur Erfassung und Verinnerlichung von Strukturen, beispielsweise des Zwanzigerfeldes. Jedoch sollte die nicht-zählende Anzahlerfassung über Strukturen das Ziel des Anfangsunterrichts sein (Padberg & Benz, 2011, S. 32ff.).
Mit Hilfe der strukturierten Darstellungen im Zwanzigerfeld können die Lernenden zudem Stützpunktvorstellungen verschiedener Anzahlen, wie 5, 10 oder 20, aufbauen. Haben die Kinder die Strukturen der Darstellungen verinnerlicht, müssen sie die Anzahl der Objekte nicht mehr zählend ermitteln, sondern können die Menge in Teilmengen, durch Ausnutzung der Teil-Ganzes-Beziehungen, zerlegen, um die Gesamtanzahl schneller bestimmen zu können (Padberg & Benz, 2011, S. 36).
Neben den Darstellungen im Zwanzigerfeld sollten auch weitere Strukturierungsmöglichkeiten einer Menge an Plättchen, beispielsweise entsprechend der Würfelbilder oder geometrisch, von den Kindern erstellt und miteinander, im Hinblick auf die schnelle Erfassung der Anzahl, verglichen werden.
Zahlverständnis Anfangsunterricht - Plättchen ordnen
Ausgangsaufgabe
Finde (geschickt) verschiedene Möglichkeiten die Zahl ... zu zerlegen.
Durch das Finden verschiedener Möglichkeiten eine Zahl zu zerlegen, wird die Einsicht in Teil-Teil-Ganzes-Beziehungen gefördert. Durch konkrete Handlungen am Material, wie das Zerschneiden von Punktestreifen oder das Auseinanderbrechen einer Stange aus Steckwürfeln sowie bildliche Darstellungen mit verschiedenfarbigen Plättchen, kann die Zerlegung von Mengen und damit von Zahlen veranschaulicht werden.
Die Systematisierung und schriftliche Notation der gefundenen Zerlegungen ermöglicht es den Kindern Beziehungen zwischen den verschiedenen Zahlzerlegungen einer Zahl zu erkennen.
Die Kenntnis verschiedener Zahlzerlegungen einer Zahl sowie der Beziehungen zwischen diesen sind eine zentrale Voraussetzung für ein gesichertes kardinales Zahlverständnis. Weiterhin sind sie notwendig für die Nutzung operativer Rechenstrategien, wie die Nutzung von Tauschaufgaben, Nachbaraufgaben oder das schrittweise Rechnen.
(Padberg & Benz, 2011, S. 41f.)
Zahlverständnis Anfangsunterricht - Zahlzerlegungen
Ausgangsaufgabe
Schreibe und male alles auf, was dir zur Zahl 8 einfällt.
Die Umwelt der Kinder ist durch Zahlen und Mengen geprägt, weshalb die Kinder bereits vor der Einschulung mit vielfältigen Darstellungen in Berührung kommen. Diese gilt es im Anfangsunterricht genauer in den Blick zu nehmen.
Durch die Betrachtung und Sammlung verschiedener Mengen und deren Strukturierungen, Zifferndarstellungen und Aufgaben mit dem Ergebnis einer zuvor festgelegten Zahl, wird der Blick der Kinder auf verschiedene Darstellungsformen von Zahlen gelenkt. Dabei findet zudem eine vielschichtige Vernetzung zwischen den einzelnen Darstellungsformen, aber auch innerhalb einer Darstellungsform, beispielsweise beim Vergleich verscheidener Mengen bestehend aus derselben Anzahl verschiedener Objekte, statt.
Bei der Betrachtung verschiedener Zahldarstellungen werden unterschiedliche Zahlaspekte gefördert. Beispielsweise durch
-
Anzahlen von Objekten einer Menge (kardinaler Zahlaspekt)
-
Preise der Waren im Supermarkt (Maßzahlaspekt)
-
Hausnummern der Häuser in einer Straße (Codierungszahlaspekt)
(Krauthausen & Scherer, 2007, S. 8f.; Selter & Zannetin, 2018, S. 30)
Zahlverständnis Anfangsunterricht - Zahldarstellungen
Weiteres Material finden Sie auf den Partnerprojektseiten mit dem Materialfinder
Testen Sie Ihr Wissen zu dem Thema mit unserem Kira-Check
